経路アルゴリズムを検討した話 その１
2013 年 11 月 28 日 by 山平頭の体操のようなゲームでも作ってみようかと思い、構想を練ってみました。
【ルール】
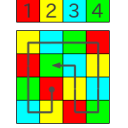
- NxMのマス目に色のタイルが並んでいる
- 色に順番がある（例：赤→黄→青→緑→赤に戻る）
- 順番通りにタイルをタップすると消える
- 一筆で全タイルが消えればクリア
シンプルなので面白いかどうかはささっとプロトタイプを作って評価してやろう、と考えました。
まずは「一筆でNxMのマスを埋めるアルゴリズム」が必要なのですが、いわゆる迷路アルゴリズムのような感じでネットで紹介されてるものを拝借することにします。
ですが、何という名前で調べればよいのかも分からないので、一筆書きから辿って探してみます。
ある連結グラフが一筆書き可能な場合の必要十分条件は、以下の条件のいずれか一方が成り立つことである（オイラー路参照）。
早速「オイラー路」というキーワードを見つけました。
どんどん調べていきます。
オイラー路とは、グラフ（グラフ理論）の全ての辺を1度だけ通る路のこと。全ての辺を1度だけ通る閉路は、オイラー閉路という。この名称は、レオンハルト・オイラーにちなむ。
～中略～
グラフGの頂点をすべて通る閉路はハミルトン路という。
確かに今回のアルゴリズムが一筆書きとちょっと違う気はしていました。
1マスを1点としてマス同士をつなぐ四方に線が伸びていると考えると、「全ての辺」ではなく「全ての点」を通る問題を解くアルゴリズムが必要である、ということが（今）分かりました。
与えられたグラフがハミルトン路を含むかどうか判定する問題は、NP完全。与えられたグラフがハミルトングラフかどうか判定する問題については、ハミルトン閉路問題を参照のこと。
む…難しい。
軽い気持ちで調べてみたものの、何だかどんどん難しくなってきてしまいました。
今回はここまでです。
タグ: アルゴリズム
