«
»

数理最適化超入門 〜 その３ 〜

2022 年 12 月 12 日 by ueno-suguru 
【前回】
前回は、機械学習と数理最適化の差について、
個人的な意見を述べた後、扱った具体例に対して、
数理モデルを実装するための問題を作成して終わりました。
【概要】
本記事は、数理最適化問題を考えるまでの
モチベーションに関する内容のその３となっています。
また、具体例を通して、

　・数理最適化の概念を感覚的にとらえられるようになる
　・「数理最適化問題を解くためのPythonによる実装」への興味が生まれる

この２点を目標としています。


今回は、以下の問題を通して、実装等に注目していきたいと思います。
【問題】
お弁当やさんでは、お弁当Xとお弁当Yを作っています。
今日は、近くの総合運動公園でスポーツ大会があり、
たくさんのお弁当が売れるだろうと見込んでいます。
お弁当Xとお弁当Yを作るのに、ほとんどの材料が豊潤にあったのですが、
お米と鶏肉だけ在庫が少なく、2つのお弁当をそれぞれ何個作ると、
売り上げが最大となるのか判断に困りました。
そこで、次のように在庫量など、
状況を整理した上で最適化問題に落とし込んで、解決したいと考えました。

=== 条件 ===
(1)お米は、在庫に40kgある。
(2)鶏肉は、在庫に60kgある。
(3)お弁当Xを１個作るのに、お米が300g、鶏肉が200g必要である。
(4)お弁当Yを１個作るのに、お米が200g、鶏肉が400g必要である。
(5)お弁当Xの販売価格は、300円である。
(6)お弁当Yの販売価格は、400円である。

【本編】

〜 Pythonで数理モデルを実装する 〜
上記条件で、問題を解くために必要な情報がそろっているので、
数理モデルを実装して、問題を解いていこうと思います。
※数理的な部分とコードの対応関係は、実装コードの後で確認します。

以下、実装全体です。
# 1.必要なライブラリの読み込み
import pulp

# 2.解くべき問題の種類を指定する。
problem = pulp.LpProblem('LP', pulp.LpMaximize)

# 3.変数の定義
x = pulp.LpVariable('x', cat='Continuous')
y = pulp.LpVariable('y', cat='Continuous')

# 4.制約式の定義
problem += 300 * x + 200 * y <= 40000　# お米の量に関する制約
problem += 200 * x + 400 * y <= 60000 # 鶏肉に関する制約
problem += x >= 0
problem += y >= 0

# 5.目的関数の定義
problem.objective = 300 * x + 400 * y

# 6.定式化した問題を解く
status = problem.solve()

# 7.最適化計算の結果確認
print('Status:', pulp.LpStatus[status])

# 8.解と目的関数の値を表示
print('x=', x.value(), 'y=', y.value(), 'obj=', problem.objective.value())

次が、出力結果となります。
最適解(Optimal)が求まっています。
Status: Optimal
x= 50.0 y= 125.0 obj= 65000.0
結果、お弁当Xとお弁当Yをそれぞれ、50個、125個作ると、
売り上げ金額が65000円になるようです。

さて、数理的な部分を見ていきましょう。
条件(1)を見ると、使えるお米の量に限度があります。
条件(3)、(4)から、お弁当毎にお米の消費量がわかるので、
お弁当Xとお弁当Yの個数をそれぞれ、x個、y個とすると、
使うお米の量は、300x+200y≦40000 となります。
同様にして、鶏肉に関しても(2)、(3)、(4)より
200x+400y≦60000となりますね。
あと、お弁当の個数がマイナスになることはないので、これらを実装すると、
「# 4.制約式の定義」のようなものになります。

このような条件を満たす(x、y)ってどのようなものか
イメージするのは、容易ではないと思います。
なので、これらをxy平面で図示してみると、
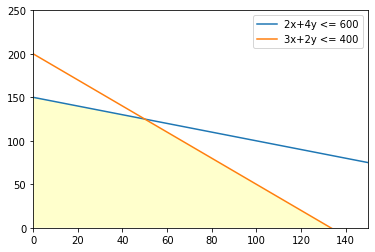
上記の黄色の領域内の(x、y)で、
「# 5.目的関数の定義」にある
300x + 400y(売り上げ価格) が最大となるものを見つけ出せば良い
ということになります。

ここで、売り上げ価格をkと表すと、
売り上げ価格は、
直線:300x + 400y = k (変形すると、y = -3/4x +k/400)
となり、切片(k/400)が最大となれば、
売り上げ価格(k)も最大になるということが見えてきます。

黄色の領域を通過する直線のうち、
切片が最大となる直線を思い描くと、次のような緑の直線になると思います。
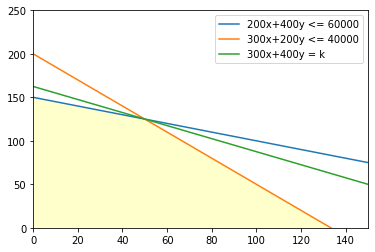
この最大となる(x、y)の組みを見つけ出しているのが
「# 6.定式化した問題を解く」
となります。

ここまでで、今回のような最適化問題を解いたことがあると、
思い出したという方もいるのではないでしょうか？
今回の題材は、高校数学で習う「線形計画法(Linear Programming)」を用いたものです。

「# 2.解くべき問題の種類を指定する。」で
「Lp」とコード上に現れていますが、この頭文字をとったもので、
今回解く問題が線形計画問題を解くという指定をしていたのでした。

問題の種類を簡単に大別すると、
線形か非線形か、
連続か離散か、
と類別できます。

数理最適化は文字通り、最適な解を算出することができ、
この連載記事を読んで頂いた方の中には、
意思決定の判断基準を大いに与えてくれるものだと感じられた人もいると思います。
ビジネスにおいては、経費削減に役立ったなどの話もチラホラ。

今、社会浸透中のAIは、このような問題まで考えてくれそうな印象を持っている人もいたかもしれませんが、
このような問題を自動的に解こうと思うと、数理最適化問題を解く数理モデルを実装する必要があります。

長くなりましたが、
これを機に数理最適化へ興味を持っていただけた方が
1人でも増えたら、大変嬉しく感じます。

興味を持たれた方の次なる学びの足がかりとして、
以下に参考図書を記載し、本連載記事を締めたいと思います。
ご精読、ありがとうございました。　

### 完 ###

=== 参考図書 ===

・「Pythonではじめる数理最適化: ケーススタディでモデリングのスキルを身につけよう」 　← 実務/実装がメイン

・「しっかり学ぶ数理最適化 モデルからアルゴリズムまで」　← 理論がメイン

数理最適化

タグ:

TrackBack